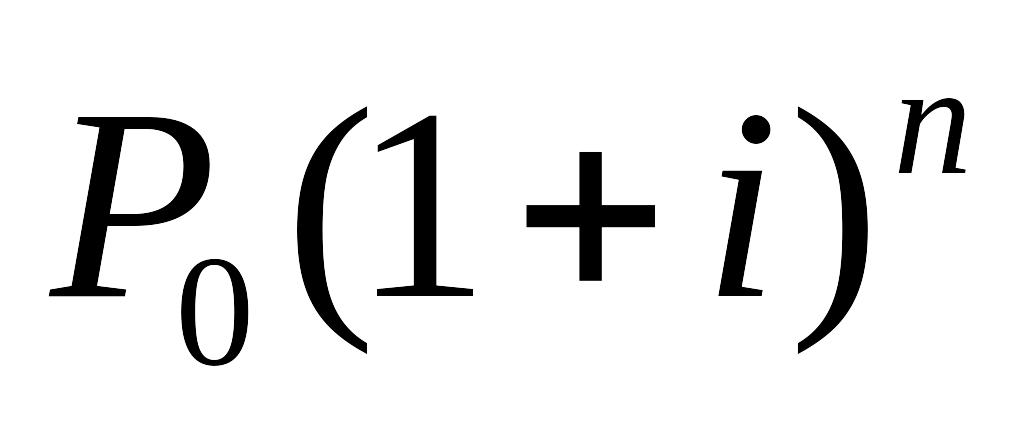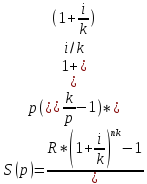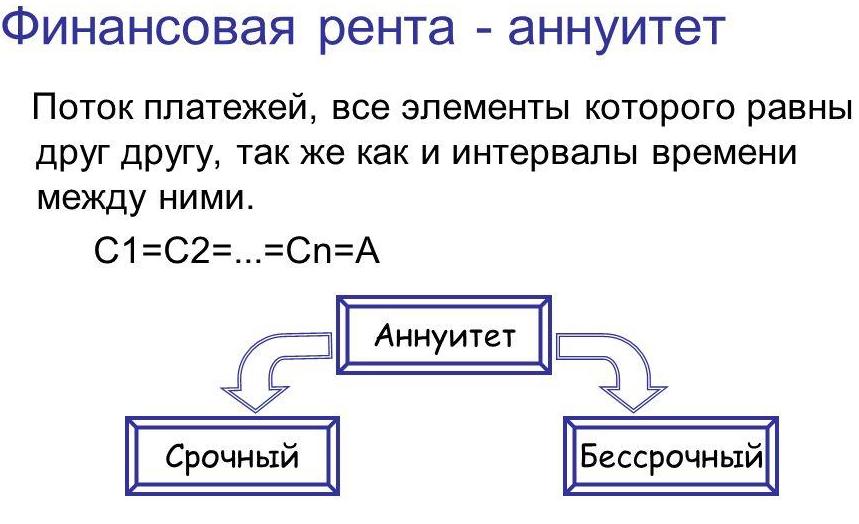
Современная величина финансовой ренты
Автор: О. Лытнев , кандидат экономических наук, доцент Калининградского государственного университета Опубликовано: 16 Сентября Несмотря на то, что общее количество формул, приведенных в трех предыдущих главах, уже приблизилось к сотне, можно смело утверждать, что это лишь малая часть того, что имеется в арсенале финансовых вычислений. Бувально по каждому из рассмотренных способов осталась масса незатронутых вопросов: ренты пренумерандо, переменные денежные потоки, использование простых процентов в анализе рент и так далее почти до бесконечности.

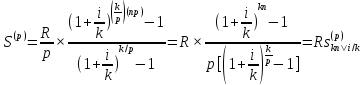




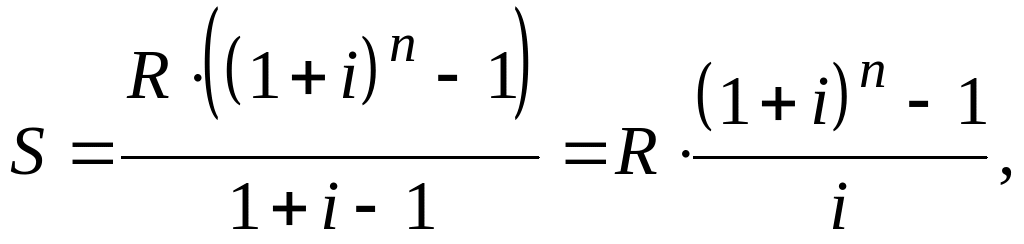
Формулы наращенной суммы. Рассмотрим наращение для различных случаев начисления рент. Обычная годовая рента. Пусть в конце каждого года в течение п лет на расчетный счет вносится по R рублей, проценты начисляются один раз в год по ставке i.






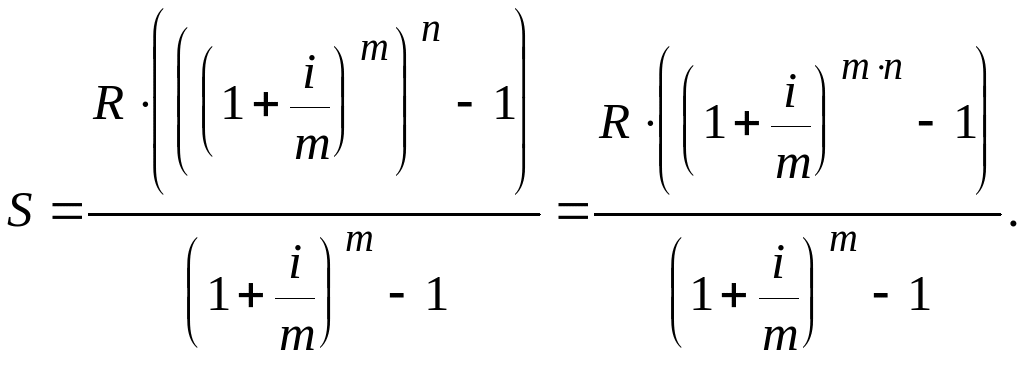
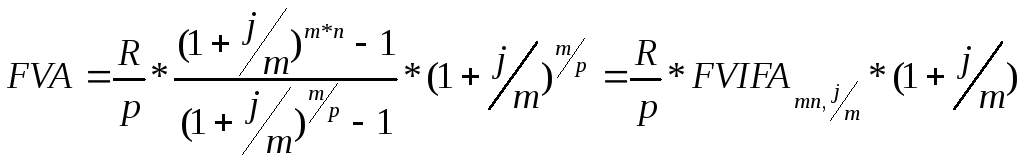

Обычная годовая рента. Пусть член годовой ренты равен R , процентная ставка i , проценты начисляются один раз в конце года, срок ренты п. Тогда дисконтированная величина первого платежа равна.