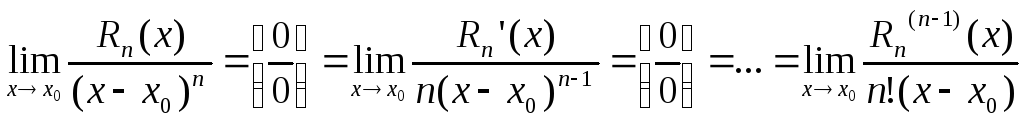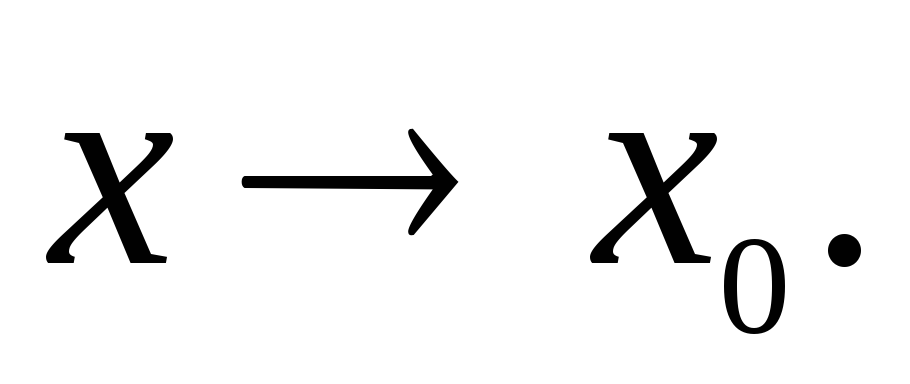ОСТАТОЧНЫЙ ЧЛЕН
В дальнейшем нам пригодится более компактное обозначение для функций, которые являются маленькими по сравнению с какими-то другими функциями. Верный ответ. Неверный ответ. А если посчитать предел, что получается?











Регистрация Вход. Ответы Mail. Вопросы - лидеры. Теоретическая механика прошу объяснить ньюанс. Лидеры категории Лена-пена Искусственный Интеллект.




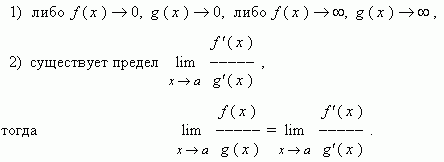






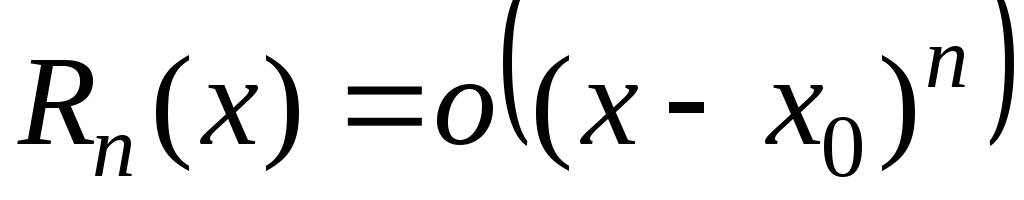

Частный случай разложения в ряд Тейлора в нулевой точке называется рядом Маклорена. Ряды Тейлора применяются при аппроксимации функции многочленами. В частности, линеаризация уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка. Обобщением понятия ряда Тейлора в функциональном анализе является ряд Фантапье. Функция называется аналитической на промежутке на множестве , если она является аналитической в каждой точке этого промежутка множества.