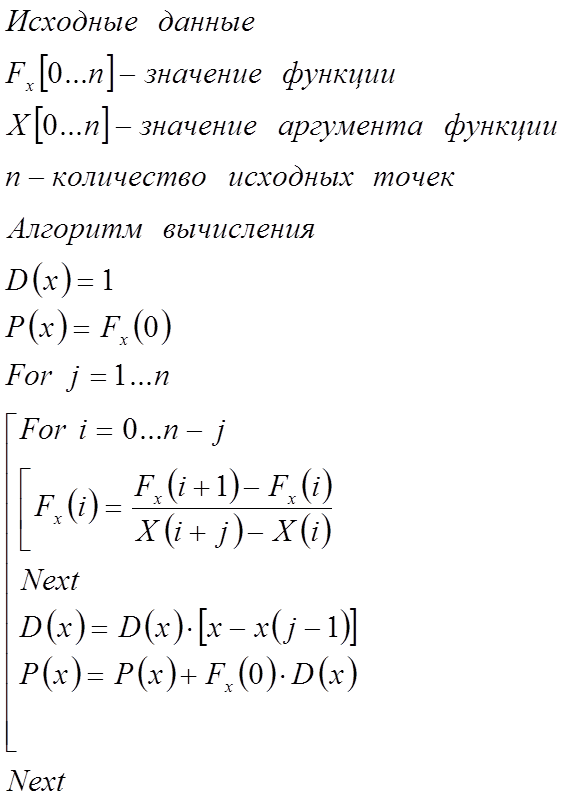Формула Тейлора с остаточным членом в форме Лагранжа и Пеано
Формула называется формулой Тейлора с центром в точке a; - остаточный член в формуле Тейлора в общем виде. Рассмотрим вспомогательную функцию. Остаточный член в форме Тейлора представляет собой б. Бесплатная лекция: " Лекция 3 " также доступна. Такую запись остаточного члена называют ост. В форме Пеано:.


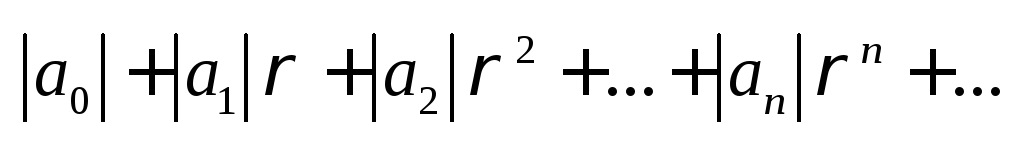






Глава 7. Дифференциальное исчисление функции одной переменной 7. Производная функции в точке 7. Дифференцируемые функции. Дифференцируемость 7.
- Лекция 8.
- Даем определения производной и дифференциала. Разбираем правила дифференцирования и выводим формулы производных для основных функций.
- Конев В. Дифференцирование функций.
- Чтобы найти первую производную в нуле, нам придётся воспользоваться определением — просто так применить стандартные правила дифференцирования не получится, так как функция по-разному опрделена в нуле и вне нуля.
- Конев В. Дифференцирование функций.
- Помочь проекту.
- В силу формулы В случае существенно комплексных z его сумму по аналогии обозначают e z.
- Определение 3. Пусть действительная функция f определена в некоторой окрестности точки x 0 и имеет в этой точке производные всех порядков.
- Разность между функцией и её многочленом Тейлора называется -м остатком , или -м остаточным членом ; обозначим этот остаток через :. Если считать, что остаток мал, то его можно отбросить без большой погрешности; при этом получается приближённая формула.
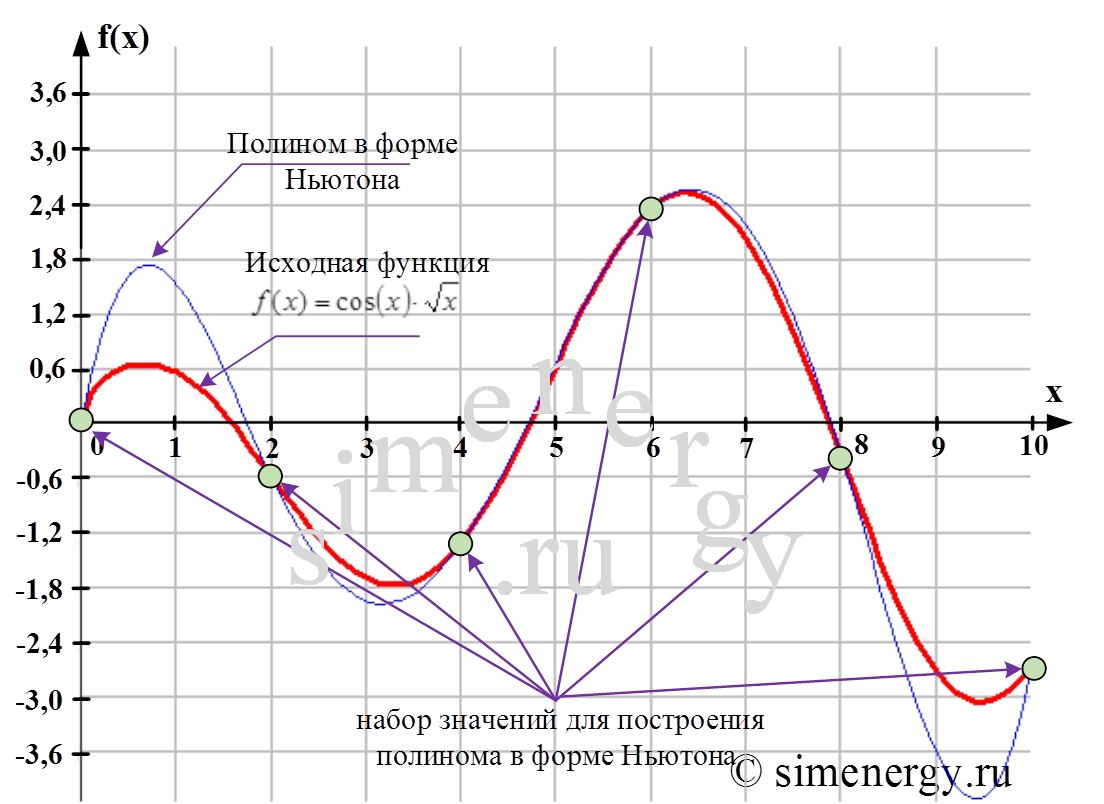



Пусть функция раз дифференцируема в некоторой окрестности точки и пусть - ее многочлен Тейлора в точке. Если обозначить , то функцию в окрестности точки можно представить формулой:. Формула 1 или 2 называются формулой Тейлора для функции в точке , а выражение - остаточным членом формулы Тейлора. Можно доказать, что остаточный член при является бесконечно малой более высокого порядка, чем.